- hillclimbing
- rely on using information about the gradient of the function to guide the direction of search
- can perform well on functions with only one peak (unimodal functions)
- can reach the top of a local maximum
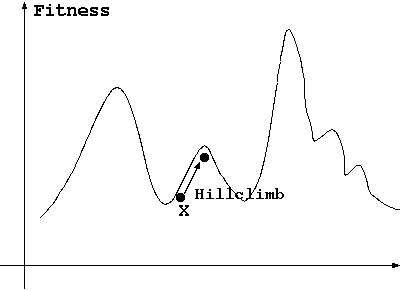
- random search and gradient search may be combined to give an iterated hillclimbing search.
- once one peak has been located, the hillclimb is started again, but with another, randomly chosen, starting point
- perform well if the function does not have too many local maxima.
- each random trial is carried out in isolation, no overall picture of the "shape" of the domain is obtained.
- therefore, this scheme is inefficient
| As its name implies, the Simulated Annealing (SA) exploits an analogy between the way in which a metal cools and freezes into a minimum energy crystalline structure (the annealing process) and the search for a minimum in a more general system. |
- SA's major advantage over other methods is an ability to avoid becoming trapped at local
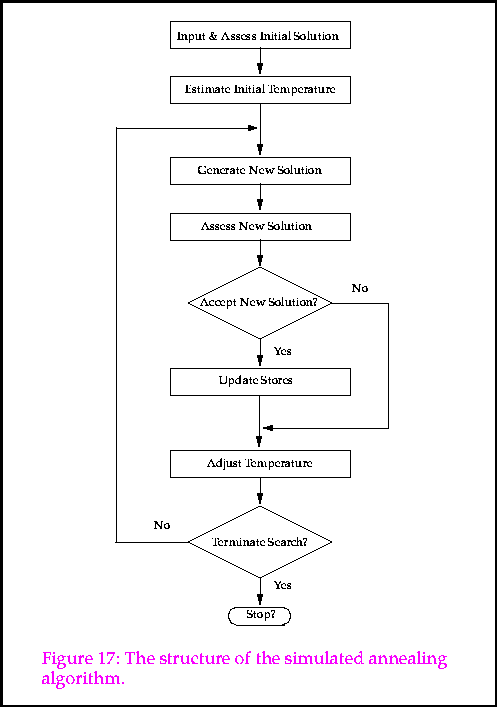
- Structure of the SA
- Basic elements
- a representation of possible solutions
- a generator of random changes in solutions,
- a means of evaluating the problem functions, and
- an annealing schedule - an initial temperature and rules for lowering it as the search progresses.
minima. The algorithm employs a random search which not only accepts changes that
decrease objective function f, but also some changes that increase it. The latter are
accepted with a probability p = exp(delta f /T) where delta f is the increase in f and T is a control parameter, which by analogy with the original application is known as the system `temperature' irrespective of the objective function involved.