XI. 交叉と突然変異
Introduction
交叉と突然変異はGAの基本的な2つのオペレータによって行われます。 GAのパフォーマンスはそれらに非常に依存しています。 タイプと実行はコード化と問題に依存します。
Crossover and mutation are two basic operators of GA. Performance of GA very depends on them. Type and implementation of operators depends on encoding and also on a problem.
交叉と突然変異の方法はたくさんあります。 この章では、いくつかの例とseveral encodingに対してそれをどのように行うかということを提案します。
There are many ways how to do crossover and mutation. In this chapter are
only some examples and suggestions how to do it for
several encoding.
バイナリーコーディング(Binary Encoding)
Crossover一点交叉 - 1つの交叉点が選ばれます、染色体の先頭から交叉点までのバイナリー文字列が1つめの親からコピーされます。残りの部分は2つ目の親からコピーされます。

11001011+11011111 = 11001111
2点交叉 - 2つの交叉点が選ばれ、染色体の先頭からはじめの交叉点までが、1つ目の親からコピーされます。はじめの交叉点から2つめの交叉点までが2つめの親からコピーされます。残りは1つめの親からコピーされます。
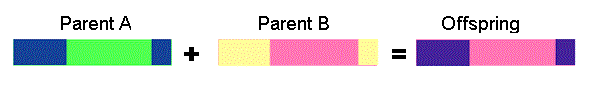
11001011 + 11011111 = 11011111
一様交叉 - 両方の親からランダムにビットがコピーされます。
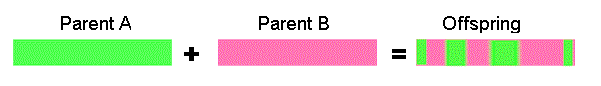
11001011 + 11011101 = 11011111
算術交叉 - ある算術作業が新しい子孫を作るために行われます。
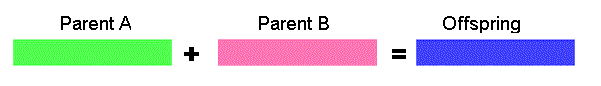
11001011 + 11011111 = 11001001 (AND)
突然変異
ビット反転 - 選ばれたビットが反転します
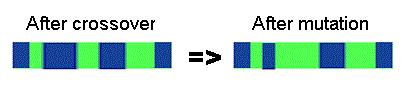
11001001 => 10001001
Crossover
Single point crossover - one crossover point is selected, binary string from beginning of chromosome to the crossover point is copied from one parent, the rest is copied from the second parent

11001011+11011111 = 11001111
Two point crossover - two crossover point are selected, binary string from beginning of chromosome to the first crossover point is copied from one parent, the part from the first to the second crossover point is copied from the second parent and the rest is copied from the first parent
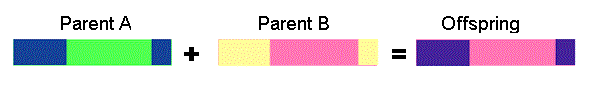
11001011 + 11011111 = 11011111
Uniform crossover - bits are randomly copied from the first or from the second parent
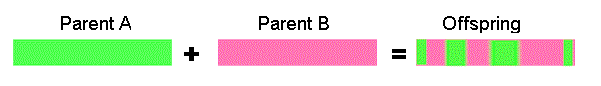
11001011 + 11011101 = 11011111
Arithmetic crossover - some arithmetic operation is performed to make a new offspring
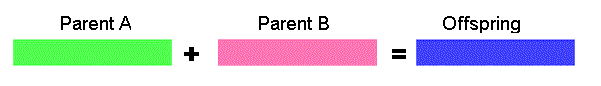
11001011 + 11011111 = 11001001 (AND)
Mutation
Bit inversion - selected bits are inverted
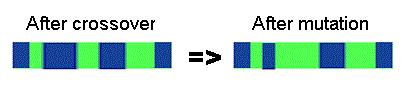
11001001 => 10001001
順列コーディング
交叉
一点交叉 - 一つの交叉点が選ばれます。はじめの親から、この交叉点までの順番がコピーされます。そして2番目の親がスキャンされ、もしその番号が子孫にないのであれば付け加えられます。
メモ: 他にも交叉点より後ろの残った部分を生み出す方法はいくつもあります。(1 2 3 4 5 6 7 8 9) + (4 5 3 6 8 9 7 2 1) = (1 2 3 4 5 6 8 9 7)
突然変異
順番を変える - 2つの番号が選ばれ、交換されます。
(1 2 3 4 5 6 8 9 7) => (1 8 3 4 5 6 2 9 7)
Permutation Encoding
Crossover
Single point crossover - one crossover point is selected, till this point the permutation is copied from the first parent, then the second parent is scanned and if the number is not yet in the offspring it is added
Note: there are more ways how to produce the rest after crossover point(1 2 3 4 5 6 7 8 9) + (4 5 3 6 8 9 7 2 1) = (1 2 3 4 5 6 8 9 7)
Mutation
Order changing - two numbers are selected and exchanged
(1 2 3 4 5 6 8 9 7) => (1 8 3 4 5 6 2 9 7)
実数値コーディング
交叉
バイナリーコーディング全て使うことができます
突然変異
加算 選ばれた値に小さな数(実数値コーディングの値に対して)に小さな値が加えられ(または引かれ)ます
(1.29 5.68 2.86 4.11 5.55) => (1.29 5.68 2.73 4.22 5.55)
Value Encoding
Crossover
All crossovers from binary encoding can be used
Mutation
Adding a small number (for real value encoding) - to selected values is added (or subtracted) a small number
(1.29 5.68 2.86 4.11 5.55) => (1.29 5.68 2.73 4.22 5.55)
木コーディング
交叉
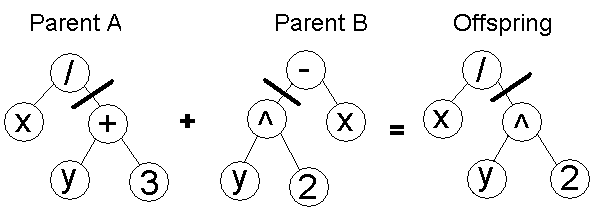
木交叉 - 両親それぞれで交叉点が一つ選ばれます。両親はその点で分けられます、そして交叉点より下の部分が新しい子孫を生み出すために置き換えられます。
突然変異
オペレータや数を変更する - 選ばれたノードが変更されます
Tree Encoding
Crossover
Tree crossover - in both parent one crossover point is selected, parents are divided in that point and exchange part below crossover point to produce new offspring

Mutation
Changing operator, number - selected nodes are changed
(c) Marek Obitko, 1998
Japanese translation (c) Ishii Manabu, 1999 - Terms of use