III. Espaço de Soluções
Espaço de Soluções
Procurar por uma solução se resume então em procurar por algum valor extremo (um mínimo ou máximo) no espaço de soluções. Às vezes o espaço de soluções pode estar bem definido, mas usualmente nós sabemos apenas poucos pontos do espaço de soluções. No uso dos algoritmos genéticos o processo de encontrar soluções gera outros pontos (possíveis soluções) à medida que a evolução acontece.
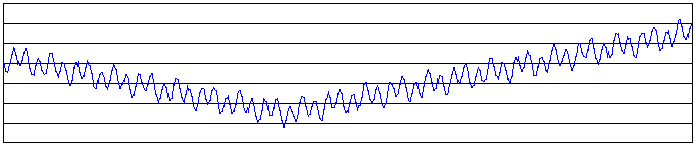
Examplo de espaço de soluções
O problema é que cada pesquisa pode ser muito complicada. Por exemplo, pode não saber por onde procurar uma solução ou por onde começar. Há muitos métodos que podem ser usados para encontrar uma solução adequada, mas esses métodos não fornecerão nedessariamente a melhor solução. Alguns desses métodos ão: subindo a montanha, pesquisa de tabelas, enrijecimento simulado e os algoritmos geneticos. As soluções encontradas por esses métodos são freqüentemente consideradas boas soluções porque nem sempre é possível provar qual é a ótima.
Problemas NP Difíceis
Um exemplo de classe de problemas que não podem ser resolvidos de modo tradicional são os problemas NP (não polinomiais).
Existem muitas tarefas para as quais podemos usar algoritmos rápidos (polinomiais), entretanto há também problemas que não podem ser resolvidos algoritmicamente.
Existem muitos problemas importantes em que é muito difícil encontrar uma solução, mas que uma vez encontrada, é fácil de ser verificada. Este fato nos leva aos chamados problemas NP-completos. O NP vem de "não polinomial determinístico" e significa que é possível "advinhar" a solução (por algum algoritmo não determinístico) e depois verificá-la.
Se tivermos uma máquina de advinhação, seremos capazes de achar uma solução num tempo razoável.
O estudo de problemas NP-completos é, por simplicidade, restrito aos problemas onde a resposta pode ser sim ou não. Em razão de que existem tarefas com saídas complicadas, uma classe de problemas chamados problemas NP-difíceis começaram a ser estudados. Essa classe de problemas não se limita aos problemas NP-completos.
Uma característica dos problemas NP é que um algoritmo simples, às vezes óbvio à primeira vista, pode ser usado para encontrar soluções úteis. Mas esta abordagem normalmente produz muitas soluções possíveis - testar todas as soluções possíveis é um processo muito lento. Para uma instância ligeiramente maior desse tipo de problema, essa abordagem é inútil.
Atualmente ninguém sabe se existe algum algoritmo rápido para encontrar solução exata para os problemas NP. A descoberta desses algoritmos permanece um desafio em aberto para pesquisadores em geral (talvez você! :-)). Atualmente muitas pessoas acham que tais algoritmos não existem e portanto procuram um método alternativo. Um exemplo de método alternativo são os algoritmos geneticos.
Exemplos de problemas NP são: problema da satisfatoriabilidade, o problema do caixeiro viajante, e o problema da mochila. Uma coleção de problemas NP está disponível aqui.
(c) Marek Obitko, 1998
Versão em Português do Brasil (c) Hermelindo Pinheiro Manoel - Terms of use