A Survey of Neural Networks: Part I

1. Overview
2. Neural Architecures and Algorithms
3. Applications

1. Overview

One of the long-standing aims of computer scientists and engineers has been, and continues to be, the design and implementation of systems which are increasingly human-like in their computational capabilities and responses. Popular culture continues to promise a future where the level of user-friendliness and intelligence built into machines would be indistinguishable from those expected from living beings. Two major avenues of research have emerged over the last two decades that aim to deliver on this promise: artificial intelligence (AI) and artificial neural networks (ANNs). While there are some similarities in both the origins and scope of both of these disciplines, there are also fundamental differences, particularly in the level of human intervention required for a working system: AI requires that all the relevant information be pre-programmed into a database, whereas ANNs can learn any required data autonomously. Consequently, AI expert systems are today used in applications where the underlying knowledge base does not significantly change with time (e.g. medical diagnostic systems), and ANNs are more suitable when the input dataset can evolve with time (e.g. real-time control systems). In order to appreciate the present excitement and interest in ANNs, it is instructive to consider the neuro-biological motivation and history of the subject.
• Biological MotivationThe chief source of inspiration for the ANN designer is the human brain, arguably the most powerful computing engine in the known Universe. Both from a computational and an energy perspective, the brain is an enormously efficient structure. It consists of some 100 billion neurons that are massively interconnected by `synapses' (estimated at about 60 trillion), and which operate in parallel. This massive parallelism overwhelms the relatively slow neuron chemistry which would otherwise lead to inefficiency - a real neuron reacts on time scales of the order of a millisecond, compared with the average silicon logic gate that switches within a nanosecond. Furthermore, the energy expenditure per neuron is only about　 Joules, compared to a microjoule for a silicon transistor: one can only speculate upon human food requirements had this figure been any higher (the brain consumes as much as 90% of all energy generated by the human body).As an information-processing system, the brain is to be viewed as an asynchronous massively-parallel distributed computing structure, quite distinct from the synchronous sequential von Neumann model that is the basis for most of today's CPUs. The term `massively-parallel' is appropriate, since the number of synapses (or interconnections) between neurons far exceed the number of neurons themselves. This is in contrast to all modern parallel computers that always have more CPUs than communication channels. Furthermore, the basic neuron is a simple computing machine, in contrast to parallel computers where each CPU is usually a complex VLSI device. Yet, in spite of this simplicity and slowness of operation, the brain is capable of tasks such as learning, cognition, perception, etc. that are beyond the scope of the most powerful electronic computers in existence. The secret of this flexibility lies in both the massive number of synaptic interconnections and the phenomenon of `plasticity' (or `adaptability'). Plasticity refers to the mechanism whereby new synaptic connections are formed between neurons, or existing synaptic connections are modified in response to a new learning experience. (Most human learning occurs within the first two years of birth when up to a million synapses are formed per second.)In order to understand the low-level operation of the brain, it becomes necessary to investigate the neuron. This was originally undertaken by neurobiologists, but has lately also been looked at in great detail by physicists, mathematicians and engineers. 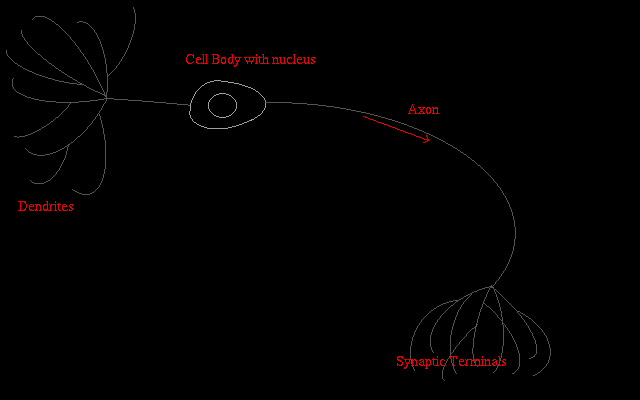For our purposes, it suffices to know that each neuron cell consists of a nucleus surrounded by a cell body (soma) from which extends a single long fibre (axon) which branches eventually into a tree-like network of nerve endings which connect to other neurons through further synapses. This is illustrated in the following schematic:
Information is transmitted from one cell to another by a complex chemical process, based on sodium-potassium flow dynamics, whose net effect is to activate an electrical impulse (action potential) which flows down the axon to other cells. When this happens, the neuron is said to have fired. Firing only occurs when the combined voltage impulses from preceding neurons add up to a certain `threshold' value. After firing, the cell needs to `rest' for a short time (refractory period) before it can fire again.
• Historical perspectiveThe story of neural networks can be traced back to a pioneering paper by McCulloch and Pitts published in 1943 that described a formal calculus of networks of simple computing elements. Many of the basic ideas developed by them survive to this day: an artificial neuron is a simple computing element that sums inputs from other neurons; a network of neurons is interconnected by adaptive paths called `weights'; each neuron computes a linear sum of the weights impinging upon it, and outputs a 1 or a 0 depending on whether this sum exceeds a preset threshold value or not. A positive value of the weight increases the chances of a 1, and is considered excitatory; a negative value increases the chance of a 0 and is considered inhibitory (real biological neurons have this property too, but with analog output values rather than binary ones).The next big development in neural networks was the publicaction in 1949 of the book The Organization of Behavior by Donald Hebbs. Hebbs, a psychologist, argued that if two connected neurons were simultaneously active, then the connection between them should be strengthened proportionally. In other words, the more frequently a particular neural connection is activated, the greater the weight between them. This has implications for machine learning, since those tasks that had been better learnt had a much higher frequency (or probability) of being accessed. In an abstract sense, learning had now been reduced to adjusting the weights between neurons to an appropriate value.In the late 1950s, Rosenblatt developed a class of neural networks called the perceptron. He introduced, furthermore, the idea of `layered' networks. A layer is simply a one-dimensional array of artificial neurons. Most current problems to which ANNs are applied to use multi-layer networks with different forms of interconnections between these layers. The original perceptron, however, was simply a one-layer architecture. Rosenblatt developed a mathematical proof, the Perceptron Convergence Theorem, that showed that algorithms for learning (or weight adjustment) would not lead to ever-increasing weight values under iteration. However, this was followed by a demonstration in 1969 (by Minsky and Papert) of a class of problems where the Convergence Theorem was inapplicable. Minsky and Papert showed that the single-layer perceptron was incapable of learning the XOR logic function - i.e. given two binary inputs, it is impossible for a perceptron to produce the exclusive-or of these as the output. They realised, however, that a multi-layer network architecture could handle XOR, but did not know of any algorithms that would train such an architecture. This work led to a considerable downsizing of interest in neural networks, which was to continue until the early 1980s.In 1982, John Hopfield, a Nobel prize winning Caltech physicist, developed the idea of a `recurrent' network, i.e. one which has self-feedback connections. Moreover, he showed that such a system could be formulated in the language of `spin glasses', an abstract assembly of dipolar magnets popular in statistical mechanics theory. The Hopfield net, as it has come to be known, is capable of storing information in dynamically stable networks, and is capable of solving constrained optimisation problems (such as the travelling salesman problem). In 1986, Rumelhart, Hinton and Williams published the `back-propagation' algorithm, which showed that it was possible to train a multi-layer neural architecture using a simple iterative procedure. These two events have proved to be the ones most responsible for the resurgence of interest in neural networks in the 1980s, up to the explosive growth industry that is today shared between physicists, engineers, computer scientists, mathematicians and even psychologists and neurobiologists.
2. Neural Architectures and Algorithms

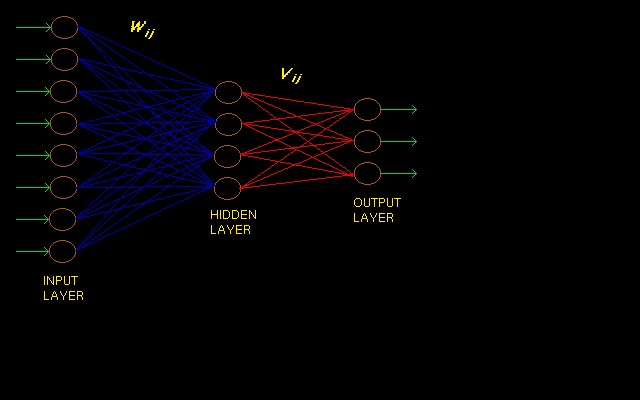
The types of problems to which modern ANNs are applied to primarily fall under the following categories:
• Recognition
• Classification
• Inference
In order for a neural network to be able to perform these tasks, it has (just like a human brain) first to be trained with some preliminary data. Training, or learning, involves a set of network input and output dataset pairs, which are usually represented as one-dimensional vectors (corresponding to the one-dimensional input and output layers of the network). The diagram below shows a typical two-layer artificial neural network (the input layer does not contribute to the layer count). Some appropriately pre-processed data is presented to the network at the input layer. The input layer neurons are not computational units, and simply propagate the input on to the hidden layer (there may be several of these in a given problem, but they all work according to the principle described here). The hidden layer and output layer neurons are simple computational units, unlike the input layer neurons. The values received at the hidden layer are the matrix product of the input vector and the 8x4 dimensional `weight matrix' W (these dimensions correspond to the number of neurons at the input layer and the number of hidden layer neurons). The matrix elements of W (simply referred to as `weights' usually) start off either as randomised values, usually between 0 and 1, or simply as 0.5. As more and more inputs are presented to the network, these matrix elements evolve under iteration according to several well-defined `learning algorithms' until the desired network output is achieved. When this happens, the network has learned a particular task. Much the same thing happens to the 4x3 dimensional matrix V. However, an important difference between this matrix and W is that V multiplies the output of actual computing elements (in the hidden layer), whereas W acts directly on the raw input data. The output of the hidden and output layer neurons is usually normalised to a value between 0 and 1 in order to preserve network stability - in most cases, this is achieved by modulating the output value of a hidden or output layer neuron by a so-called `activation function'. A good choice of this activation function is a crucial factor in the network performing as desired. Popular choices include the Heaviside step function and the hyperbolic tangent function. A trained network is capable of producing correct responses for the input data it has already `seen', and is also capable of `generalisation', namely the ability to guess correctly the output for inputs it has never seen. This property is similar to that of the human mind, which can, for example, be taught a particular alphabet and rules of pronunciation, and correctly generalise to the case of words that it has not previously seen. Generalisation is related to the `capacity' of a neural network, which refers to the maximum number of patterns that can be learned before a network starts to produce unacceptable errors. A rigorous mathematical theory of capacity was worked out in the late 1980s by Elizabeth Gardner, in the context of statistical mechanics. Other notable features of networks include the following:
• Robustness to noise: A trained network is capable of correctly recognising an input pattern even if it is corrupted by noise. Much like a human brain that can correctly infer or fill in gaps in knowledge given only a partial representation.
• Universal approximation: Formal mathematical results show that a general neural network can always be built that comes arbitrarily close to representing any multi-dimensional mathematical function.
Training algorithms come in a wide variety of flavours, but are generally divided into two camps:
• Supervised TrainingThis refers to schemes where an external agent (i.e. a computer program) monitors the input and output vector pairs and adjusts the weights in a way that pairs each input with its target output. This is analogous to learning a skill with a teacher. Popular supervised training schemes include the following:
• Hebbian learning: inspired by Hebb's work, this simply increases the weight value between any two connected neurons depending on the frequency of their being activated during training.
• Back-progagation: indisputably the most popular training algorithm in existence, back error progagation (to give it its full name) or BEP is intuitively appealing if biologically false. BEP training relies on the error between the desired and actual output being propagated back to the earlier network layers and then being used to adjust the weights, for every input-output data pair. Thus, if the error is negative (i.e. the desired value is greater than the actual output), the weight needs to be increased to narrow the difference; while if the error is positive, then the weight can be decreased correspondingly. The major problem with BEP is the large number of iterations required for an optimal stable solution to be reached - however, given a sufficiently long training period, the network will almost always train properly. The Apple Newton uses this kind of learning algorithm. While popular because of its simplicity, BEP is frowned upon by perfectionists, since the human brain uses no error correction signal during learning phases.
• Reinforcement learning: inspired by psychology experiments on animals, reinforcement learning depends upon a performance metric known as the reinforcement signal. The training iterations are designed to maximise this signal such that each correct output increases its value, while each incorrect output decreases it. Training is considered complete when the reinforcement signal does not significantly alter with each iteration.
• Unsupervised TrainingIn this scheme, only input vectors are presented to the network, and the network adjusts its own weights without the benefit of knowing what particular output to assign to a given input. Instead, unsupervised training schemes usually end up classifying the input set into distinct groupings, with each group storing those input vectors which have some degree of similarity. Clearly, this kind of training is ideal for cases where some seemingly uncorrelated data has to be classified into similarity classes. Unsupervised learning schemes typically depend on competitive activity between the output neurons, such that only one out of several neurons is active at any one time. Each active output neuron classifies correlated input data, and different output neurons will be active for different groups. Unsupervised schemes have been used in such applications as speech-driven typewriters, where they have been used to classify spoken words into particular phonetic classes. They have also been used in data compression applications, where they are used as so-called `feature extractors' which determine the most significant parts of incoming information that cannot be discarded in any attempt to eliminate data redundancy.
3. Applications

Because of the tremendous flexibility that neural network architectures possess, as well as the fact that they are influenced by such a diverse cross-section of professionals ranging from engineers to psychologists, the ANN industry is likely to continue its rapid growth for some time to come. In this section, we look at some of the more prominent uses to which ANNs have been put:
• Pattern recognition training: This is probably the biggest market for ANN technology. Automated recognition of handwritten text, spoken words, facial/fingerprint identification and moving targets on a static background have all been successfully implemented.
• Speech production:This is the opposite of speech recognition, and involves a neural network connected to a speech synthesizer. Since correct pronunciation of English depends on the context of the word, ordinary text-to-speech algorithms have an enormous set of rules to contend with. By contrast, ANN-based algorithms use the classification ability of neural networks to discover these rules for themselves. A most remarkable example of this is the program NETtalk developed by Sejnowski and Rosenberg in 1986. As training proceeds, the network first learns to distinguish vowels from consonants, then to distinguish boundaries between different words, and finally produces intelligible speech. This has been likened to the normal development of speech in humans.
• Real-time control:From an industrial perspective, this is the single most useful application of ANN technology. It is used today for monitoring complex control systems such as chemical plants. The data produced by such plants is typically a series of analog values (such as pressure, temperature, etc) that has to be kept within certain ranges. A neural network can be trained to recognise optimal values for such data, and make necessary adjustments to control valves, etc. whenever necessary.The most impressive control application to date, however, has been a neural network that has been successfully trained to drive a lorry in ordinary traffic conditions for several miles. The implications of this work for future automated transport are immense.
• Business:Several commercial ANN software packages exist today that are used by businessmen to predict stock market trends. A neural network is trained on stock prices over a certain period (this is treated as time-series input data), and the generalisation capability of the network is used to predict the likely price in the future.
• Signal processing:Mention has already been made of the use of unsupervised neural networks for data compression. This has immediate applications in one, two and multidimensional signal processing. Other applications to date have included such things as echo-cancellation, noise suppression, filtering, and others that are traditionally associated with DSP technology.