XI. Crossover and Mutation
Introduction
There are many ways how to do crossover and mutation. In this chapter are
only some examples and suggestions how to do it for
several encoding.
Binary Encoding
Crossover
Single point crossover - one crossover point is selected, binary string from beginning of chromosome to the crossover point is copied from one parent, the rest is copied from the second parent

11001011+11011111 = 11001111
Two point crossover - two crossover point are selected, binary string from beginning of chromosome to the first crossover point is copied from one parent, the part from the first to the second crossover point is copied from the second parent and the rest is copied from the first parent
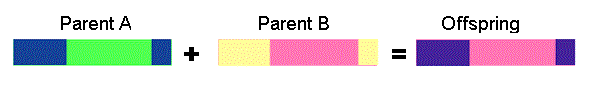
11001011 + 11011111 = 11011111
Uniform crossover - bits are randomly copied from the first or from the second parent
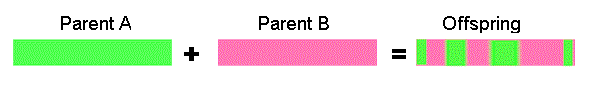
11001011 + 11011101 = 11011111
Arithmetic crossover - some arithmetic operation is performed to make a new offspring
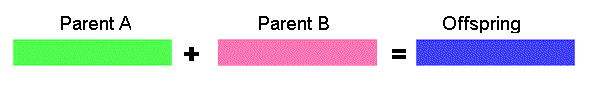
11001011 + 11011111 = 11001001 (AND)
Mutation
Bit inversion - selected bits are inverted
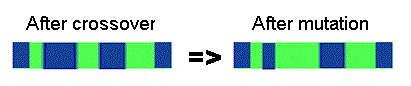
11001001 => 10001001
Permutation Encoding
Crossover
Single point crossover - one crossover point is selected, till this point the permutation is copied from the first parent, then the second parent is scanned and if the number is not yet in the offspring it is added
Note: there are more ways how to produce the rest after crossover point(1 2 3 4 5 6 7 8 9) + (4 5 3 6 8 9 7 2 1) = (1 2 3 4 5 6 8 9 7)
Mutation
Order changing - two numbers are selected and exchanged
(1 2 3 4 5 6 8 9 7) => (1 8 3 4 5 6 2 9 7)
Value Encoding
Crossover
All crossovers from binary encoding can be used
Mutation
Adding a small number (for real value encoding) - to selected values is added (or subtracted) a small number
(1.29 5.68 2.86 4.11 5.55) => (1.29 5.68 2.73 4.22 5.55)
Tree Encoding
Crossover
Tree crossover - in both parent one crossover point is selected, parents are divided in that point and exchange part below crossover point to produce new offspring
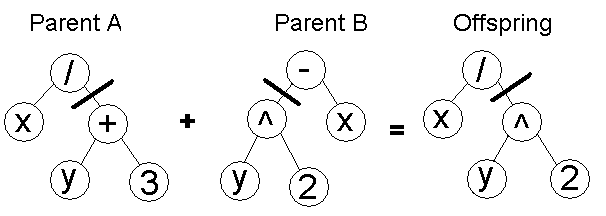
Mutation
Changing operator, number - selected nodes are changed
(c) Marek Obitko, 1998 - Terms of use